29 novembre 2009
GP de MACAU..corico !
Lire le compte-rendu de presse du Team Of Paris.
La vidéo :
25 novembre 2009
20 novembre 2009
A streamliner in Bonneville
 Aux antipodes du Shell Eco-Marathon,
Aux antipodes du Shell Eco-Marathon,une "moto" à près de 600 km/h ! (367 MPH)
Cliquez sur le titre ou ici pour parcourir le site.
18 novembre 2009
Shell Eco Européen 2010 : ça se précise...
07 novembre 2009
Moto en accélération (faible ou forte)
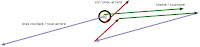
 Pour terminer, on doit vérifier le théorème de la résultante : la somme vectorielle des 3 forces doit être nulle. Ceci se traduit graphiquement par le triangle dessiné à droite. On dessine d'abord la force connue (la rouge), puis on trace les parallèles aux supports des deux forces à déterminer. L'une est tracée à l'extrémité de la force connue et l'autre à l'origine. On obtient au final la norme et le sens des deux forces recherchées.
Pour terminer, on doit vérifier le théorème de la résultante : la somme vectorielle des 3 forces doit être nulle. Ceci se traduit graphiquement par le triangle dessiné à droite. On dessine d'abord la force connue (la rouge), puis on trace les parallèles aux supports des deux forces à déterminer. L'une est tracée à l'extrémité de la force connue et l'autre à l'origine. On obtient au final la norme et le sens des deux forces recherchées. A nouveau, je vous propose de comparer la 1ère image du bras oscillant sous une faible accélération puis cette 2ème image avec une forte accélération. La comparaison est délicate dans la mesure où le bras apparaît plus petit dans le second cas à cause du maintien de la même échelle des forces par rapport à la taille des pièces.
A nouveau, je vous propose de comparer la 1ère image du bras oscillant sous une faible accélération puis cette 2ème image avec une forte accélération. La comparaison est délicate dans la mesure où le bras apparaît plus petit dans le second cas à cause du maintien de la même échelle des forces par rapport à la taille des pièces.
 commodité, regardez l'image où les deux situations d'accélération apparaissent en même temps.
commodité, regardez l'image où les deux situations d'accélération apparaissent en même temps. On voit bien que malgré la grande différence de tension de chaîne et de force exercée par le sol sur le pneu, la force exercée par la biellette de suspension et en conséquence la force de compression de l'amortisseur ne changent presque pas.
On voit bien que malgré la grande différence de tension de chaîne et de force exercée par le sol sur le pneu, la force exercée par la biellette de suspension et en conséquence la force de compression de l'amortisseur ne changent presque pas. Je n'oublie pas l'action de la chaîne mais la distance de celle-ci par rapport à l'axe de pivotement varie assez peu en comparaison.
Je n'oublie pas l'action de la chaîne mais la distance de celle-ci par rapport à l'axe de pivotement varie assez peu en comparaison.06 novembre 2009
Moto 2 : elles arrivent....
Moto en accélération d'intensité variable
Ci-dessous, une vidéo plus complète avec le calcul des forces exercées sur la chaîne et les suspensions (traction de chaîne, force de compression de l'amortisseur arrière et force axiale sur la fourche).
Attention, ces calculs sont encore faits à suspensions figées ! Imaginez que le ressort d'amortisseur arrière et les ressorts de fourches sont des tubes très rigides en acier...
Malgré cette restriction, les résultats sont intéressants, comme par exemple la quasi constance de la force de compression de l'amortisseur. En regardant de près, on peut même constater (comme c'est curieux !) que celui-ci est moins comprimé si l'accélération augmente !
En effet, comme je le signalais dans un précédent message, la force exercée par le sol sur le pneu arrière s'incline de plus en plus avec l'accélération et sa direction se rapproche de l'axe de bras oscillant, diminuant ainsi le bras de levier et donc la force exercée sur l'amortisseur.
Bonne lecture !
05 novembre 2009
04 novembre 2009
Moto en accélération constante
Sur cette animation vous pourrez voir comment on peut calculer les forces exercées sur les pneus d'une moto en accélération constante, en ligne droite.
Pour commencer simplement, quelques hypothèses simplificatrices :
- l'ensemble moto + pilote est considéré indéformable, les suspensions sont figées
- la résistance au roulement est négligée (la force exercée par le sol sur le pneu avant est considérée verticale)
- les effets aérodynamiques sont négligés (valable si on ne roule pas trop vite !)
- la moto roule en ligne droite sur un plan parfaitement horizontal
La video montre les vecteurs forces obtenus en fonction de la position avant / arrière du centre de gravité G pour une accélération donnée.
Ici l'accélération est de 0,7 g. La force d'inertie horizontale dirigée vers l'arrière a donc une norme égale à 70 % du poids. Cette force d'inertie et le poids forment une résultante inclinée vers l'arrière et vers le bas.
Suivant le principe de d'Alembert, ce problème de dynamique peut donc être résolu comme un problème de statique à 3 forces :
- résultante poids + force d'inertie (connue)
- force sol / pneu arrière (à déterminer)
- force sol / pneu avant (verticale)
Ces 3 forces sont donc coplanaires. Leurs supports sont concourants car les supports de la résultante poids + inertie et de la force sol /pneu avant se coupent. On obtient ainsi la direction de la force exercée par le sol sur le pneu arrière.
Pour terminer la résolution, on doit vérifier que la somme vectorielle des 3 forces est nulle. Cela se traduit graphiquement par le triangle que vous verrez sur la video.
On obtient ainsi les 2 forces recherchées.
Deux limites dans ce "pseudo équilibre" (oui ça bouge donc ce n'est pas un équilibre statique) :
- limite wheeling : si le centre de gravité est trop en arrière, la force sur le pneu avant diminue jusqu'à zéro d'où perte d'appui de l'avant. "Équilibre" sous l'action de 2 forces : résultante poids + inertie et forces sol / pneu arrière. On ne peut pas aller plus en arrière pour une accélération donnée.
- limite patinage (de la roue arrière motrice) : si le centre de gravité est trop en avant, la force sol / pneu arrière doit s'incliner fortement vers l'avant. On ne peut dépasser une certaine inclinaison qui dépend de la valeur du coefficient d'adhérence (piste sèche ou piste humide...). Pour un facteur = 1 on aurait une inclinaison maximale de 45° (tan 45° = 1).
Prochainement, je montrerai l'influence de la variation de position en hauteur du centre de gravité mais si vous avez compris ce chapitre vous pourrez en deviner les conclusions.
Beaucoup plus tard si je suis courageux je vous montrerais ce qui se passe si on prend en compte les mouvements de suspension ou les effets aérodynamiques.
Enfin, nous pourrons calculer les forces sur les sous-ensembles : axes de roues, chaîne, bras oscillant, tés de fourche...etc.
Remarque : comme pour le calcul précédent (forces appliquées à l'arrêt) les forces calculées sont strictement indépendantes de l'architecture de la moto en ce qui concerne ses suspensions. Que la moto ait des suspensions ou non et quel qu'en soit le principe on obtiendra ce résultat !
C'est important de comprendre cette remarque avant de se faire des noeuds à la tête.
MAIS, bien sûr, quand on fera (promis j'essaierai !) une simulation dynamique avec prise en compte des mouvements des suspensions, l'évolution de ces forces sera variable suivant les systèmes : fourche télescopique, système triangulé...etc.
Dans tous ces raisonnements, il faut bien comprendre que pour faire le bilan d'un équilibre (ou ce que j'appelle "pseudo équilibre" pour une accélération constante en ligne droite) on fait l'inventaire des actions mécaniques EXTÉRIEURES agissant sur le système isolé.
Ici, le système isolé est "La moto + son pilote". Les actions entre le bras oscillant et l'amortisseur sont des actions INTÉRIEURES au système, donc elles n'interviennent pas.
Pourquoi ? Simplement parce que si A et B sont des pièces de l'ensemble isolé (exemple A = bras oscillant et B = biellette de suspension), si on prend en considération la force "A sur B" alors il faut aussi prendre la force "B sur A". Pourquoi plus l'une que l'autre ? Au final, la force "A sur B" et la force "B sur A" s'annulent ! Pourquoi donc s'embarrasser ? On les ignore dès le début !
Pour compléter la vidéo n°1 dans laquelle le centre de gravité est déplacé d'avant en arrière, voici la video n°2 dans laquelle on modifie la hauteur du centre de gravité.
On fait ainsi apparaitre
- une limite "basse" : c'est la limite de patinage.
- une limite "haute" : c'est la limite du wheeling.
En pratique, si la piste est humide, il vaut mieux que le centre de gravité soit rehaussé (par rapport à un réglage neutre "sec").
Si la piste est sèche et les pneus très performants alors on peut avoir un centre de gravité plus bas.
Ces remarques étant valables pour ce qui concerne l'efficacité en accélération de la moto.
Aujourd'hui, l'adhérence est phénoménale et la force exercée par le sol sur le pneu arrière peut être fortement inclinée vers l'avant (environ 63° avec un facteur de 2 car TAN (63,43°)= 2 ).
Remarque : Au lieu de mettre G à 1m de l'arrière et 50 cm en hauteur on aurait pu "choisir" 80 cm et 40 cm mais ce n'est pas plus faisable ! Imaginez maintenant les conséquences dramatiques au freinage avec un centre de gravité aussi avancé ! On comprend bien pourquoi la roue arrière se lève aussi facilement (pas avec moi mais avec un vrai pilote !) au moment du freinage...
03 novembre 2009
Statique moto : forces à l'arrêt
Sur cette animation, vous pourrez voir l'influence de la position avant / arrière du centre gravité sur les forces exercées par le sol sur les pneus arrière et avant. En réalité, le centre de gravité ne se déplace pas autant mais l'exagération du déplacement permet de mieux observer le phénomène.
Ce problème de statique se résoud assez facilement. Il s'agit d'un problème d'équilibre à 3 forces parallèles, verticales :
- le poids de l'ensemble moto + pilote (vertical, vers le bas)
- la force sol / pneu arrière (vertical, vers le haut)
- la force sol / pneu avant (vertical, vers le haut)
La somme vectorielle de ces forces est nulle. Donc la norme du poids est égale à la somme des normes des forces exercées par le sol sur les pneus.
La somme des moments (par rapport à un point, par exemple le centre de gravité G) est nulle.
Si on note :
FA la norme de la force sol / pneu arrière
FB la norme de la force sol / pneu avant
LA la distance entre la direction de FA et le centre de gravité G
LB la distance entre la direction de FB et le centre de gravité G
On a donc FB.LB - FA.LA = 0
(moment = norme de la force x bras de levier)
Dernière remarque : ce calcul de force est strictement indépendant de l'architecture de la moto, fourche télescopique ou non, suspensions ou pas. Ce qui compte :
- le poids total
- la distance (mesurée horizontalement) entre le centre de gravité et le point de contact des pneus sur le sol. La moto étant supposée placée sur un plan parfaitement horizontal, la hauteur du centre de gravité ne rentre pas en ligne de compte.
Bien évidemment, si le centre de gravité est au milieu des 2 roues alors le poids se répartit équitablement à 50% (la moitié donc !) sur chaque pneu. Pas besoin de démonstration fumeuse pour le comprendre. L'animation ci-dessus permet d'apprécier la proportionnalité des forces à la distance du poids par rapport aux points d'appui, entre "tout à l'arrière" et "tout à l'avant".
 Please,
Please,